Thales

Inhalt

Thales von Milet

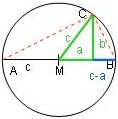
Es sei ein Kreis um M gegeben, von einem Punkt C auf der Peripherie werde das Lot auf den Durchmesser (2c) gefällt, dann haben wir das rechtwinklige Dreieck (a;b;c)
Das Dreieck A;B;C ist nach dem Thalessatz rechtwinklig, die Höhe darin ist b.
Nach dem Höhensatz ist das Quadrat über der Höhe genauso groß wie das Produkt aus den Hypothenusenabschnitten, also

Den Rest erledigt ihr spielend selbst.

Thales von Milet (624-546 v.Chr.) soll in Milet (Westküste Kleinasiens, heute Türkei) berühmter Philosoph, Mathematiker usw. gewesen sein. In der Antike galt er als der Älteste der sieben Weisen, das waren hochangesehene Politiker, Philosophen und so. Um ihn ranken sich viele Geschichten, ähnlich wie um unseren Pythagoras. Auch von Thales gibt es keine schriftlichen Aufzeichnungen, warum auch immer. Ob er denn je existiert hat, ist nicht gewisser als bei Pythagoras.

Aber es gibt in der Mathematik den wichtigen Satz des Thales:

Jeder Peripheriewinkel über dem Durchmesser eines Kreises ist ein rechter Winkel.

Die Winkel bei C bis G (von unendlich viel weiteren) in der Abbildung sind alles Peripheriewinkel über dem Kreisdurchmesser (AB) und somit rechtwinklig. Das gilt selbstverständlich für den unteren Halbkreis auch.

Den Beweis führen wir hier nicht, es geht um Beweise für den Pythagorassatz.
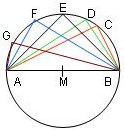
Aber es gibt da noch so eine kleine Geschichte: Der Mathelehrer wurde aus dem Unterricht gerufen. Damit die Schüler lange zu tun haben, stellte er die Aufgabe, möglichst viele rechtwinklige Dreiecke zu konstruieren. Ein Schüler kannte den Thalessatz und wandte ihn an, natürlich wurde er Sieger im internen Klassenwettbewerb. Sein Name: Carl Friedrich Gauss. Eine Garantie auf den Wahrheitsgehalt der Story kann ich nicht liefern.