Inhalt
Pythagorasbaum
Stammbasis ist das Quadrat mit der Seitenlänge a (erste Ebene), darauf das rechtwinklige gleichschenklige Dreieck, an dessen Katheten die Quadrate mit den Seitenlängen b (2. Ebene) usw. Die Quadrate mit der Seitenlänge d sind in der 4. Ebene.
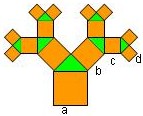
15 Quadrate zählen wir in obiger Abbildung, berechne deren gesamte Flächeninhalte
abhängig von a.
1. Ebene: A1 = a2Der weitere Weg sollte nun nicht schwierig sein.
2. Ebene: A2 = 2b2 = a2 (Pythagoras)
Also A1 + A2 = 2a2
Der nächste Baum hat 5 Ebenen, weitere Ebenen machen Verdichtungen in den Zweigenden deutlich.
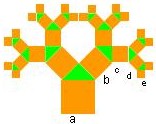
Für die Bäume benutzten wir ein gleichschenkliges Dreieck, das ergibt symmetrische Bäume, andere Winkel als 45° ergeben unsymmetrische Bäume.
Hier ein Baum, in dem ein Winkel des rechtwinkligen Dreieckes 300 ist:
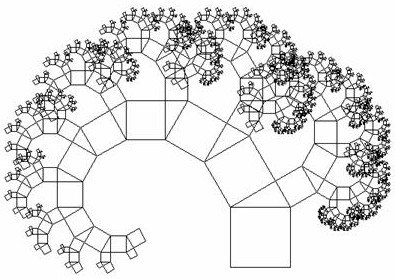
Solche Bäume erzeugt man z.B. mit der empfehlenswerten Software
WinFunktion, Mathematik plus 14, bhv Software. Siehe unter www.bhv.de